DEFINICIÓN DE FUERZAS SUPERFICIALES Y FUERZAS MÁSICAS(definición del Teorema de Cauchy).

 

Fuerzas de superficie y fuerzas de cuerpo.

 Teorema de Cauchy.

 

Aguiar Hernández Ismael.

NUMERO DE CONTROL: 21310175.

 

TECNOLOGICO NACIONAL DE MEXICO

INSTITUTO TECNOLOGICO DE LA PAZ

 

FUNDAMENTOS DE MECÁNICA DEL MEDIO CONTINUO

 

Doc. Jorge Moore Valdivia.

 

Ingeniería Civil. 4^to – E.

 

La Paz, Baja California Sur,03 de marzo del 2023.

Introducción.

El contenido presentado a continuación, es un ensayo en el cual se argumentan las definiciones de fuerzas superficiales, fuerzas másicas o de cuerpo y la teoría de Cauchy, así como los postulados de la teoría. De la misma forma se ven aplicadas las leyes de newton, como la conservación de la energía y el principio de acción y reacción.

Todos estos conceptos van implicados en el análisis del medio continuo, por lo que se le da seguimiento en el área de la física e ingeniería civil, en donde se estudian mediante cálculos que darán como resultado el efecto o deformación que producen las fuerzas al medio continuo o a un punto x del mismo, por lo que se ve relacionado con varias ramas de la ingeniería civil, estas son asignaturas como mecánica de suelos, dinámica, hidráulica, modelación, todas aquellas donde se ve relacionado el estudio del comportamiento de la partícula, para así poder tomar decisiones con respectivos fundamentos.  

Como sabemos estas fuerzas se analizan aplicadas a un medio continuo, el cual es un conjunto infinito de partículas, estudiadas sin considerar posibles discontinuidades,  son fuerzas representadas como cantidades vectoriales que se describen como concepto intuitivo de empujar o tirar al volumen, o masa que es el medio continuo en general o aplicada a una partícula P que seria las fuerzas de superficie o de contacto a diferencia de las fuerzas másicas que afectan a distancia a todo el volumen del medio continuo. Estas fuerzas se describirán argumentaran y se compararan para identificar las diferencias.

Recordemos que un medio continuo o también considerado curva cerrada esta definido por un contorno, siendo este el que nos permite identificar la deformación (Aplicación de fuerzas) y realizar cálculos, como también poder demostrar el teorema de Cauchy de una mejor manera.  

A diferencia del contorno que envuelve a todo el medio continuo, es decir lo define, este cuenta con partículas infinitas las cuales serán analizadas y representadas por P.  

Se ilustra claramente los conceptos para poder tener una mejor captación del lector y ejemplificación de la información.

Desarrollo.

A continuación, se argumentará como se relaciona, cual es el apoyo que brindan los siguientes conceptos y teorías a la ingeniería civil, de igual manera al campo académico de estudiantes de ingeniería civil.

Comenzando con la definición de fuerzas superficiales, se considera a las fuerzas que están distribuidas en la superficie del cuerpo como consecuencia o producto del contacto con otros cuerpos. Argumentando la definición en el libro de mecánica de medios continuos para ingenieros por Xavier Oliver Olivella menciona que son “Aquellas fuerzas que actúan sobre el contorno del volumen del material considerado. Pueden considerarse producidas por las acciones de contacto de las partículas situadas en el contorno del medio con el exterior del mismo.” (Olivella)

Ilustración 1 Representación de fuerzas másicas (Mecánica de medios).

            Algunos ejemplos de estas fuerzas son las fuerzas debidas a la presión de contacto entre dos cuerpos, el rozamiento, el empuje del terreno sobre un muro, las fuerzas de impacto (Mecapedia, n.d.)

            Como se mencionaba las fuerzas de superficie son acciones distribuidas en una superficie específica en el contorno del sólido o dentro de él, que actúan por contacto directo con otro cuerpo. Estas fuerzas por unidad de área se representan mediante el vector t* = t_i*e_i. (Web Academica, n.d.)

Por lo tanto, en la ingeniería civil estas fuerzas pueden ser analizadas como los efectos del viento a una estructura, las cargas puntuales, esfuerzos cortantes, así como el conocimiento aplicarlo en el estudio de mecánica de materiales y dinámica, donde se analiza el comportamiento de las partículas.

A diferencia de las fuerzas de superficie tenemos a las fuerzas de cuerpo o también conocidas como fuerzas másicas, consideradas como las acciones distribuidas en el volumen del sólido, las cuales actúan a distancia (es decir, no a contacto), podemos ejemplificarlo con las fuerzas gravitacionales, de inercia o magnéticas. Un cuerpo al estar expuesto a una inercia se le ejerce toda la fuerza vectorial al volumen del cuerpo. Argumentando con la definición propuesta por Xavier Oliver “son fuerzas que se ejercen a distancia sobre las partículas del interior del medio continuo. Ejemplo de dichos tipos de fuerzas son las fuerzas gravitatorias, las inerciales o las atracciones magnéticas” (Olivella).

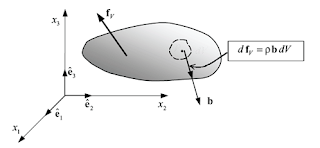
Ilustración 2 Representación de fuerzas másicas (Mecánica de medios).

Aclarando que las fuerzas de cuerpo son fuerzas que actúan sobre todos los elementos de volumen de un medio continuo y están distribuidas a través de todo el cuerpo (Masa). Las fuerzas de gravedad y de inercia son los ejemplos mejor conocidos.

 Tales fuerzas se representan como una cantidad vectorial b = biei   que indica la fuerza por unidad de masa. Considerando una densidad constante del cuerpo ρ, la fuerza de cuerpo por unidad de volumen se escribe como ρb = ρbiei   (Web Academica, n.d.)

En la ingeniería civil se puede calcular este tipo de fuerza y ver como someten a las estructuras o comportamiento de las partículas mismas, como el cálculo a la exposición a un cuerpo magnético, que repela o atraiga la partícula, al fuerza gravitatoria en la caída de un cuerpo o como este puede deformar el medio continuo, así mismo en las asignaturas de la carrera de ingeniería civil es importante aclarar este concepto y mentalizar como se puede aplicar y cuando un medio continuo está siendo sometido por una fuerza másica.

Objetivo de tener las ideas más precisas y poder diferenciar una fuerza de otra. (Mecánica de medios)

Para el análisis de fuerzas es mejor tener un claro concepto de ellas por lo que, en mecánica de medios continuos son consideradas cantidades vectoriales que se describen mejor mediante conceptos intuitivos tales como empujar o tirar. 

De acorde a la ilustración 1 y 2. Las siguientes expresiones matemáticas para denotar las fuerzas.

 Formulas obtenidas al realizar sustitución y despejes información en libro de mecánica de medios continuos para ingenieros. (Mecánica de medios)

 Por último, mencionar el teorema de Cauchy, manteniendo en cuenta la aplicación en un medio continuo, este define que es el medio o curva cerrada sobre el que actúan las fuerzas másicas y de superficie, con el objetivo de poder deducir las ecuaciones que modelizan la deformación de un medio continuo sujeto a la acción de alguna fuerza externa y/o interna.

“Dichas ecuaciones surgen de principios o leyes de conservación físicos, tales como el principio de conservación de la masa, de la energía, del momento, etc.” (MODELIZACIÓN MATEMÁTICA Y SIMULACIÓN, n.d.)

            En el teorema de Cauchy se implementa la ley de la conservación de la misma forma el principio de reacción y reacción donde se considera la 3ra ley de newton.  El estudio se centra en considera una partícula P del interior del medio continuo y una superficie arbitraría, que pasa por dicho punto P realizando un corte de normal unitaria “n” en dicho punto.  Recordando el medio continuo como una masa o volumen el cual es cortado por esta superficie dividiéndolo en dos partes clasificadas como volúmenes materiales, donde la superficie de corte se contempla como parte del volumen de cada volumen material.

    En esta superficie de cómo se puede notar en la parte derecha de la ilustración 3, se aprecia la aplicación de fuerzas superficiales de contacto que hay entre los dos volúmenes materiales, lo que nos permite realizar el cálculo en el punto P y conocer el comportamiento de la partícula en ese punto. 

Ilustración 3 Teorema de Cauchy, volúmenes materiales. (Mecánica de medios)

    En la anterior ilustración podemos observar las fuerzas que actúan sobre el punto P, las cuales con las fuerzas de tracción y la normal unitaria, expresadas como vectores los cuales presentan dependencia, como de cuál sea la particular(será diferente para cada caso), influirá también la rotación de la superficie (la rotación es definida a través de la normal n) igualmente depende de cual sea la superficie del corte del medio continuo es decir el campo vectorial dependerá de la normal n viéndolo aplicado a un campo de vectores. 

El autor Francisco Periago Esparza menciona la aplicación de los vectores de tracción t y normal n respecto al punto P o partícula. “En Física e Ingeniería el tensor de tensiones es el rey de la fiesta debido a la gran cantidad de información que proporciona. En efecto: como hemos dicho antes, en las aplicaciones, la tracción representa a las fuerzas superficiales que actúan sobre cada punto x del medio continuo. Una vez tenemos a nuestra disposición el tensor, para determinar la fuerza que actúa sobre el punto x en la dirección n el tensor de esfuerzos proporciona toda la información sobre el estado tensorial del medio.” (Esparza, 2003)

Es importante considerar los ingredientes fundamentales de la teoría de Cauchy, estos son el 1er y 2do postulado de Cauchy. En el primero el vector tracción t que actúa en un punto material P de un medio continuo, según un plano de normal unitaria n, depende únicamente del punto P y de la normal n. Lo que argumenta lo antes mencionado de la dependencia del vector tracción con la normal n, como se muestra en la ilustración 4.  En el segundo postulado también conocido como principio de acción y reacción, el vector tracción en un punto P de un medio continuo, según un plano de normal unitaria n, es igual y de sentido contrario al vector de tracciones en el mismo punto P según un plano normal unitario -n en el mismo punto, es decir que con la misma fuerza que se acciona se reacciona pues fue dividido permitiendo analizar al medio continuo en ese punto. A continuación, se observa en la ilustración 5. (Olivella)

Ilustración 3   1er postulado de Cauchy. t=t (P, n) y 2do postulado de Cauchy. t (P, n) =- t=t(P, -n)

          

 Conclusión.

            De acuerdo con lo señalado y presentado anteriormente, se obtuvo el conocimiento de las diferencias entre fuerzas másicas y fuerzas superficiales, se consideran a las fuerzas másicas como la fuerza que actúa sobre todo el cuerpo del medio continuo, por lo que son conocidas como fuerzas de cuerpo, ejemplo de ella tenemos a las fuerzas gravitacionales, que actúan a distancia a lo contrario de las fuerzas de superficie que actúan en un punto especifico del medio continuo y se consideran de contacto ejemplo tenemos a las fuerzas de rozamiento. Otro de los temas abordados fuer el tema de teoría de Cauchy la que divide al medio continuo en un punto P para analizar las fuerzas de torción respecto a la normal n y las fuerzas de tracción considerando la ley de conservación y el principio de acción y reacción.

            Mencionando la importancia que tiene en el ámbito ingenieril es muy grande pues estos conceptos y principios se ven involucrados en la gran parte de ramas relacionadas con la ingeniería, pues ayuda a realizar el análisis de los medios continuos, es decir el comportamiento que tiene la partícula de distintos materiales, por ejemplo que tanta fuerza produce una deformación, como se ve afectada, permitiendo al ingeniero poder tomar decisiones fundamentadas en el comportamiento de los materiales involucrados en la modelación o cálculos estructurales, para llegar a la corrección o aprobación de los mismos.

Es importante recordar, para luego aplicar en otras asignaturas más adelantadas, que las fuerzas son aplicadas a un campo vectorial, esto quiere decir que toda la representación será dada en vectores, lo que nos permite relacionar los temas de la unidad pasada, con la divergencia, y rotacional, para poder demostrar donde se está aplicando una fuerza (una fuente) y donde se está contrarrestando (un sumidero) de la misma manera al aplicar el teorema de Cauchy se puede analizar mediante la normal el vector rotacional, especificado en ese punto, como se mencionada nos permite conocer el comportamiento de la partícula en dicho punto del medio continuo.

            Concluyendo con la importancia de realizar análisis a profundidad como se contemplan en un medio continuo, para lograr ser un buen ingeniero que tenga sustento para defender sus cálculos al poder describir el comportamiento ante las fuerzas que pueden causar deformaciones al medio en cuestión.

 

 

Bibliografía.

(s.f.). En X. o. olivella, Mecánica de medios continuos para ingenieros (UPC ed.). Politex. Recuperado el 01 de febrero de 2023, de https://upcommons.upc.edu/bitstream/handle/2099.3/36197/9788498802177.pdf

Esparza, F. P. (2003). MODELIZACIÓN MATEMÁTICA Y SIMULACIÓN. Recuperado el 01 de Marzo de 2003, de https://www.dmae.upct.es/~fperiago/apuntes_docencia/apuntes_curso_04.pdf

Mecapedia. (s.f.). Recuperado el 01 de Marzo de 2023, de http://www.mecapedia.uji.es/pages/fuerzas_de_superficie.html#:~:text=Se%20denominan%20fuerzas%20de%20superficie,El%20rozamiento

MODELIZACIÓN MATEMÁTICA Y SIMULACIÓN. (s.f.). Recuperado el 02 de Marzo de 2023, de https://www.dmae.upct.es/~fperiago/apuntes_docencia/apuntes_curso_04.pdf

Olivella, X. O. (s.f.). Mecanica de medios continuos para ingenieros . Edicions UPC. Recuperado el 01 de Marzo de 2023, de https://upcommons.upc.edu/bitstream/handle/2099.3/36197/9788498802177.pdf

Web Academica. (s.f.). Recuperado el 01 de Marzo de 2023, de https://webacademica.com/descripcion-del-esfuerzo-fuerzas-de-cuerpo-y-fuerzas-de-superficie/